女儿数学成绩非常不理想。可想而知写数学作业的时候，抓耳挠腮，各种不情愿。效率质量无从谈起，完不成作业的时候，也是家常便饭。可是丑媳妇总要见公婆，也不可能每次都这么侥幸，最终要面临老师的审查。于是乎作业不带，各种借口就编出来了。从这做法来看，孩子还是有点脑子的。不过对于家长和老师来说，太小儿科了。最终老师微信找了我多次。无奈要自己出手帮孩子复习知识点。

昨天的作业的题目中有这样三道计算题：

• 1+2+3+4+5+…+100
• 1+3+5+7+9+…+99
• 4+8+12+16+…+100

题目1，我先说下背景。这里面有个故事是关于伟大数学家高斯的。当时他有一个比较懒的老师，老师为了打个盹，就让孩子们算下1+2+3+4+5+…+100的结果。主角光环的高斯很快就算出结果5050了。老师的休息下的计划也这样泡汤了。

1. 面积方法

为直观的用图形展示出来，我们先把题目换成 1+2+3+4+5+6+7+8+9+10。我们每个数看成一个方格。第一行1方格，第二行2个方格，第三行3个方格。那么这个时候图形是这样的。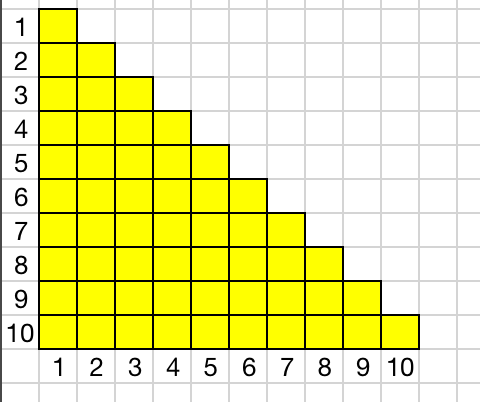

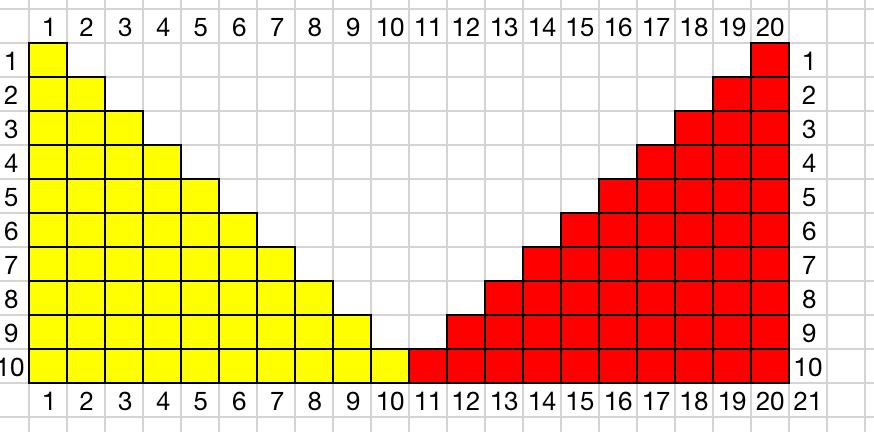
这个时候，我们看下这个图形的影子是什么样的。

这个时候，如果我们把一个图形旋转后合并在一起，是不是会变成这个样子？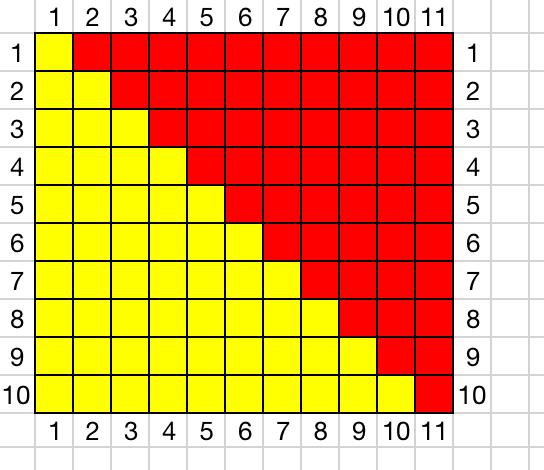

这个时候问：方格的面积是多少？这个估计小朋友们都会了。面积=长×宽。 那么黄色部分是不是就是1+2+3+4+5+6+7+8+9+10的结果那？
需要注意的地方，图形的长是11(10+1). 黄色部分的面积= 11 × 10 ÷ 2=55. 这个时候我们再算 1+2+3+4+5+…+100 = 101 × 100 ÷ 2= 5050。 是不是这样不用记公式了，其实当年的等差公式，我也早还给老师了。个人比较喜欢这个方法，对孩子来说更加直观一些。
我们这个时候再来算算 1+2+3+4+5+…+n 是不是就可以直接说结果了 。 1+2+3+4+5+…+n = (n+1) × n ÷ 2

2. 平均数方法

平均数 = 和 ÷ 个数(项数) 那么 和 = 平均数 × 个数(项数).
1+2+3+4+5+…+100 我们可以清晰的知道数的个数一共是100个，那这100个数的平均数是多少？

同样我们简化下, 1 2 3 这三个数 2 恰好在中间，也就是1 2 3 的平均数。
我们再看下偶数个数 1 2 3 4 ，那个这四个数的平均数是不是位于2和3的中间也就是2.5。这个数也就是(1+4) ÷ 2

其实平均数 = (第一个数 + 最后一个数)÷ 2
那么1+2+3+4+5+…+100 是偶数个，平均数位于50与51之间，也就是 50.5 。也就是 (1+100)÷ 2

1+2+3+4+5+…+100= (1+100) × 100 ÷ 2

3.两列相加法（名字可能不准确）

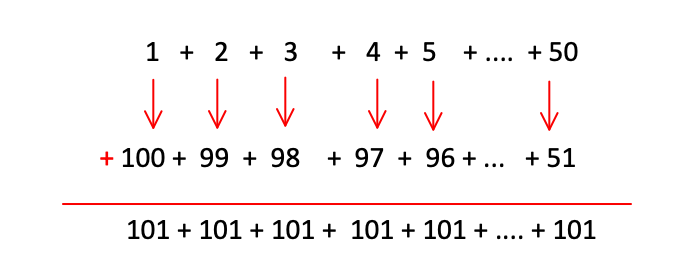
这个方法也是孩子比较能理解的方法。我们把数写成列成一列，我们在把上面的一列顺序反过来写在下面。我们用上面的数与下面的数相加。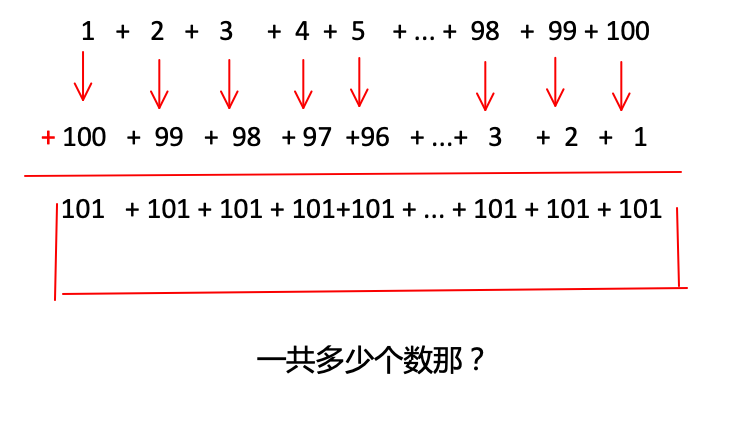

那么上图的结果是多少那？ 101 × 100. 由于我们多加了一倍。这个时候我们将结果÷ 2 也就是 101 × 100 ÷ 2

4. 配对法(名字可能不准确)

我们把第一个与最后一个，第二个与倒数第二个以此类推进行相加。就会得到下图。这样的数一共50个。所以结果就是 101 × 50.其实我不喜欢这个方式，我就傻傻的闹不清是50个这样的数，还是51个这样的数，还是49个。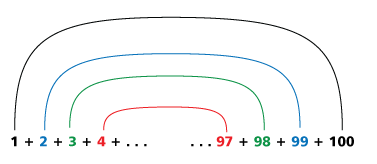

这里还有另外一种划法，同样是两列：由于数是偶数两个，我们恰好可以平均分成两列，如下图。101的个数恰好是50个。结果也就是 101 ×

这个时候如果遇到个数是奇数个，我们这个时候可以借助0，使用0 进行占位，凑够偶数个。如 1+2+3+4+5+6+7+8+9 就可以画成下面的样子
0 1 2 3 4
9 8 7 6 5
然后就可以计算了 结果= 9*5

5. 等差公式法

这个方法对于孩子来说，应该属于天书级别的。sum = n ×(n+1) ÷ 2 如果让孩子死记硬背这样的公式，就是典型的扼杀孩子的创造力。故不推荐，但是对于成年人来说，接受度普遍偏高。

方法介绍完了，那么让我们来看下作业的题目。

1. 4+8+12+16+…+100

猛看与1+2+3+…+100 毫无关系. 我们看下面的，是不是可以找到规律

4= 4 × 1
8 = 4 × 2
12= 4 × 3
…
100= 4 × 25

那么 4+8+12+16+…+100 = 4 ×1 + 4 × 2+4 × 3 +…+ 4 × 25 根据乘法分配率 = 4 × (1 + 2 + 3 … + 25) = 4 × (25 x 26 ÷ 2)=1300

2. 1 + 3 + 5 + 7 + … + 99

方法一：1 + 2 + 3 + 4 + … + 100 = (2 + 4 + 6 + … + 100) + (1 + 3 + 5 + 7 + … + 99)
我们前面已经计算出了 1 + 2 + 3 + 4 + … + 100 到100 是 5050 , 2 + 4+ 6 + …+ 100 我们计算出了是 2550 。那么 1 + 3 + 5 + 7 + … + 99 = 5050-2550 = 2500

方法二：1 + 3 + 5 + 7 + … + 99 如果每一个数与2的的关系可以写为
= (2×1-1) + (2×2-1) + (2×3 -1) + (2×4-1) + … + (2×50 -1)
根据加法结合律，我们可以得出
= (2×1 + 2 × 2 + 2×3 + 2×4 + …+ 2×50) - (1 + 1 + 1 + 1 + … +1)
我们根据 2×1 + 2 × 2 + 2×3 + 2×4 + …+ 2×50 可以清楚的看到数的项是50个，也就是说 减去的1的项数共50个。那么
= (2×1 + 2 × 2 + 2×3 + 2×4 + …+ 2×50) - 1×50
=2×（1+2+3+4+…+50) - 50
= 2 × 50 × 51 ÷ 2 - 50
= 2500

方法三： 我们根据两列相加法 。我们可算出每对是100. 那么有多少对那？ 由于 我们可以从方法1中清晰看到，100个数被分成了偶数和奇数，也就是数奇数共50个

= 100 × 50 ÷ 2
= 2500
方法四：根据公式法，1+ 3 + 5 + 7 + … + 2 * n -1 的和就是 n × n 也就是n的平方。 99 = 2 × 50 -1 即 n = 50 .所以可以轻松的计算出 1 + 3 + 5 + 7 + … + 99 = 50 × 50 = 2500

变化的题目

• 5 + 6 + 7 + 8 + … + 100
• 50 + 52 + 54 + 56 + … 100