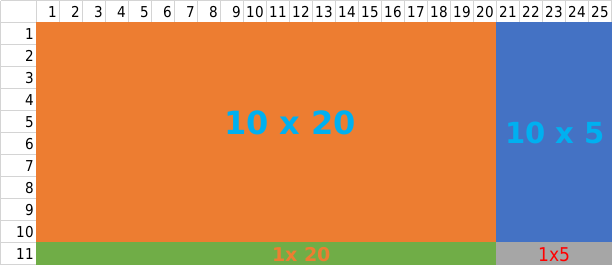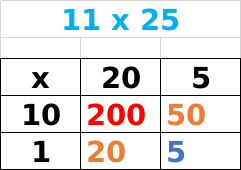11的速算口诀：两边一拉，中间相加

11与两位数相乘的计算方法

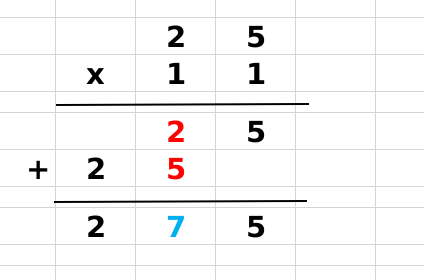
11 × 25 = 275

• 方法一： 竖式计算过程：

11 × 25 的计算中，我们可以清楚的看到2放到百位上，5放到了个位上，十位的2与个位的5相加，放到了中间十位上。如果中间的十位满十，就需要进位。即2与5分别放在了两边，中间是 2+5 。

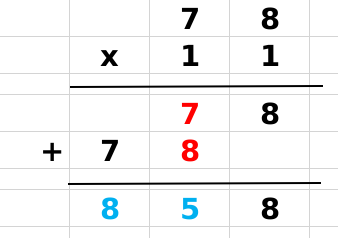
11 × 78 = 858 ，7与8放两边，中间是7+8. 满十进位，心算过程可为 7(7+8)8 => 7+1)58> 858 竖式验算：

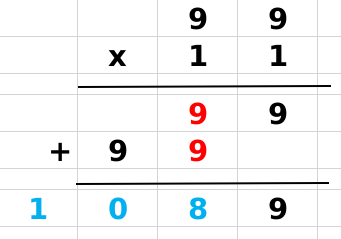
11 × 99 = 1089 ，9与9放两边，中间是(9+9)，满十进位，心算过程可为 9(9+9)9 => (9+1)89 => 1089 竖式验算：

• 方法二： 面积法计算过程

11 × 25 既两个数相乘，我们可以看做求解面积。我们为了同时推到其他公式，将图形分为下面的样子。

从图中我们可以得出，该图形共有4部分组成。分别是： 10 × 20 + 10 × 5 ,+ 1 × 20 + 1 × 5 那么

面积 = 10 × 20 + 10 × 5 + 1 × 20 + 1 × 5
= 200 + 20 +50 + 5
= 200 + (20 + 50) + 5
= 200 + 70 + 5
从上面我们可以看出200的2就位于百位上，70 的7 恰好位于十位上 ，5在个位上。

11 × 25 = (10 + 1) ×(20 +5) = 10 × 20 + 10 × 5 + 1 × 20 + 1 × 5

根据图形我们可以推导出下面的公式：

(a + b ) × (c + d) = a ×c + a ×d + b ×c + b ×d
看过这个面积法，对于图形法计算会更加容易理解。

• 方法三：图形法

图形方法也是一个比较有意思的方法。将数拆分为容易计算的部分，然后进行运算。其中图形法也有一种变种，不过没有这里的太好理解。故不再介绍。

• 方法四：结网计数法

结网计数法需要画较多的线，如果遇到带8与带9的相乘，非常乱，并且不容易数节点的数量，非常容易数错。比起竖式法差的太远了。

综上：乘法计算有多种方法，不过竖式法是最优雅的方式。一些特殊的计算，记住规则可以达到速算的目的。面积法非常有利于速算情况的推导。后面其他的速算，我们将主要使用面积法推导

11与多位数乘法速算推广

运算： 415 × 11 = 4565

解析： 答案的第一个数字为被乘数的第一个数字4，第二个数字为被乘数前两个数字(4+1)的和，三个数为被乘数后面两个数字(1+5)的和，最后一个数字(5)为被乘数最后一个数字。

运算： 13212 × 11 = 145332

关于速算的一点建议：记住速算的这些规则，最好的方式是在理解的基础上通过习题进行加强巩固。每天做上一道，用不久就熟记在心了。

关于9乘法的有趣乘法补充

接上篇中九的乘法口诀速记方法，后来发现9的一个有趣的乘法。12345679被称为有趣的”缺8数“，它与9相乘，结果是九个1组成的九位数。

12345679 × 9 = 1111111111

知道这个规律，稍微更改下：

• 12345679 × 18 = 12345679 × 9 × 2 = 222222222
• 12345679 × 27 = 12345679 × 9 × 3 = 333333333
• 12345679 × 36 = 12345679 × 9 × 4 = 444444444
• 12345679 × 54 = 12345679 × 9 × 6 = 666666666
• 12345679 × 81 = 12345679 × 9 × 8 = 888888888

这种规律是需要记忆的。

                1 × 9 + 2  =  11
              12 × 9 + 3  =  111
            123 × 9 + 4  =  1111
          1234 × 9 + 5  =  11111
        12345 × 9 + 6  =  111111
      123456 × 9 + 7  =  1111111
    1234567 × 9 + 8  =  11111111
  12345678 × 9 + 9  =  111111111
123456789 × 9 + 10 = 1111111111

一个比较有意思的是：1的位数就等于前面相加数字